| swiss-algebra-help.com |
 |
||
Rational NumbersFrom: http://www.resonancepub.com/oops.htm The Explosion of the Ariane 5On June 4, 1996 an unmanned Ariane 5 rocket launched by the European Space Agency exploded just forty seconds after its lift-off from Kourou, French Guiana.
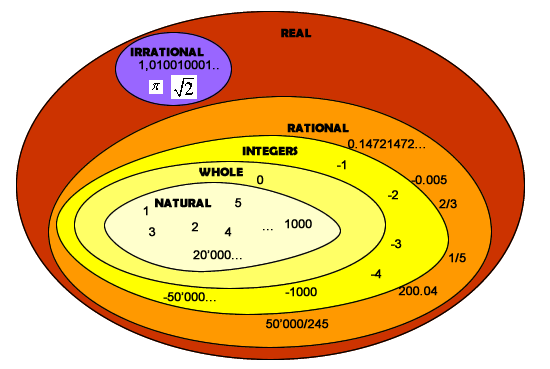
Rational numbers are those numbers formed as ratio of two integers. Take the integers 2 and 3 for instance. you can create a rational number like:
The above number is read "two" over "three" or "two thirds". In algebra you can use it as it is but if you want to actually "use" it in a calculator its value (derived from dividing 2 by 3) is 0. 666666... where the dots mean that the number 6 is repeated infinitely. So you need to approximate the number to say 2,3 digits after the point. However, this can lead to catastrophic mistakes using software and wrong approximations (see story on the right- hand side) In our case, 2/3 is a decimal number with a "periodic sequence"; the integer 6 repeating forever.So they include also repeating decimals (0.666...) and terminating decimals (such as 0.4 i.d 2/5). But they can be, just numbers like 1,2,3,4...and 0 since the bottom integer can be 1 as well. In other words, we can say that all integers are also rational numbers. Moreover, they form a system called Q [2] where division is always possible, except for zero [1] CAREFUL The "bottom" number of a rational number cannot be zero ! This is simply because you cannot divide a number by zero (try with the calculator; you will get an error message). To express the same idea, how can you separate 10 apples in groups of zero apples? It's a logical nonsense. The calculator will refuse to continue if you do divide any number by zero. In algebra, you say that it is a number that can be expressed as
Conclusions A rational number is called this way because it's a ratio between two integers Rational numbers form a system of numbers where division is always possible except for zero.
You might be interested... There is a whole branch of mathematics called "Number Theory" which study the properties of numbers and their intrisic relations, especially of integers. More exactly "number theory is largely concerned with properties of the set of positive integers, and as such has a considerable overlap with algebra... One the of the foundation stones of number theory states that every positive integer can be written in exactly one way as a product of prime numbers" [1].This fundamental properties of positive numbers has been applied in computer cryptography to develop security codes. So, some mathematicians just do that, they "play" and look beyond number for more meanings and laws. Isn't is a more relaxed way of looking at mathematics?
Source:
From rational numbers back to the algebra homework help webpage
|
On the shore of a vast sea
|
||
BlogOnline Calculator
Pre-AlgebraAlgebra
On what we standToolsStay in touch with nature. It's full of mathematics! 
Enjoy This Site?
Then why not use the button below, to add us to your favorite bookmarking service? |
|||
|
| Homepage| About Us |Study Tips |Contact | This Website is Powered by Site Build It! - and I would never use anything else.
|
|||
|
| |||
The rocket was on its first voyage, after a decade of development costing $7 billion. The destroyed rocket and its cargo were valued at $500 million. A board of inquiry investigated the causes of the explosion and in two weeks issued a report. It turned out that the cause of the failure was a software error in the inertial reference system. Specifically a 64 bit floating point number relating to the horizontal velocity of the rocket with respect to the platform was converted to a 16 bit signed integer. The number was larger than 32,768, the largest integer storeable in a 16 bit signed integer, and thus the conversion failed. 
is their set
