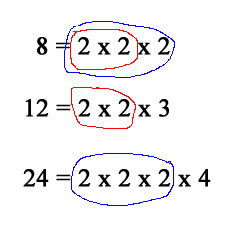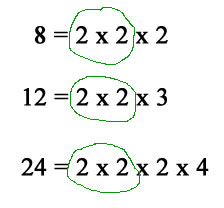| swiss-algebra-help.com |
 |
|
Greatest Common FactorThe Greatest Common Factor
The acronym GCF is often used. In order to find the GCF you must first find the prime factors of the integers, and then compare what they have in common and take their largest factor.
So, the GCF between 8 and 12 is (red marks) 2 x 2 = 4 the GCF between 8 and 24 is (blue marks) 2 x 2 x 2 = 8 the GCF between 8, 12 and 24 is....do you know?
The Greatest Common Factor is a concept easier to understand than its name is to remember, yet not so easy to digest immediately, really. Like for the whole of mathematics and algebra, You must exercise it! It is of paramount importance in algebra. It helps simplify fractions. It goes together with the Least Common Multiple (LCM). Here is a calculator for you to use for both calculations (use it NOT as shortcut, but as way to check your manual answers!) 16 MEMORABILIA MATHEMATICA rupted movement of thought, with distinct intuition of each DESCARTES. Rules for the Direction of the Mind, Philosophy 220. Analysis and natural philosophy owe their most impor- A Philosophical Essay on Probabilities [Tru- 221. There is in every step of an arithmetical or algebraical MILL, J. S. Source: Source: Free JavaScripts provided
From the greatest common factor (GCF) back to homepage
|
On the shore of a vast sea
|
|
|
Stay in touch with nature. It's full of mathematics! 
Enjoy This Site?
Then why not use the button below, to add us to your favorite bookmarking service? |
||
|
| Homepage| About Us |Study Tips |Contact | This Website is Powered by Site Build It! - and I would never use anything else.
|
||
|
| ||