Fractions as Measure

Fractions as measure. Yes, an easy way to understand fractions is the idea of measuring the length of an object.[1]

Here, the how much is involved an not "how many parts" [2].

Let's take a ruler

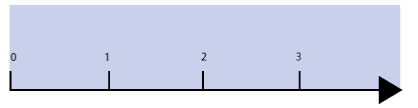
You can see that a ruler is basically the same as the number line pictured here below.

The Number Line:

The introduction of the concept of the number line can illustrate that there are infinite fractions between two fractions. And so of course infinite rational numbers between any two of them.

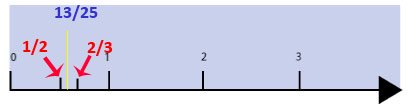
An example of an application of fractions as measure.

Say we must measure something very accurately, how can we find two fractions equally spaced between say 1/8 and 1/9 (of an inch)?

Here is the answer from a fifth grade pupil who practiced extensively with the number line for two years [3] (simplified)

First of all, 1/9 is smaller than 1/8 and so comes first on the number line. Fractions are "backwards".

You, see? We cannot see the solution because the fractions don't have the same unit (the denominator, the number "at the bottom").

So, how can we see a common denominator? Well. by finding a common ground between the different partitions of the two fractions.

And how? Well, by means of the first equal divisions which please both fraction: in other words, the Least Common Denominator (LCD).

You will see that once you subdivide your fraction (part-whole concept) you will get an apparently "new" fraction ( and equivalent fraction) because the numerator has changed too.

	1/3	original partitions (3) Denominator=3 Numerator (red area) = 1 partition
	2/6	2 times the original partions (6) Denominator=6 Numerator (red area) = 2 partitions
	4/12	4 times the original partions (12) Denominator=12 Numerator (red area) = 4 partitions

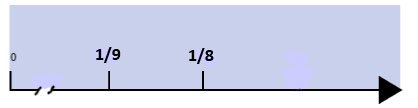
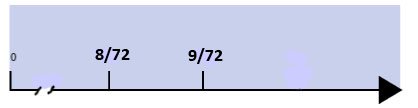
Coming back to our original problem, in order to find the new common ground multiply the denominator and modify the rest (the numerator) accordingly!

So 9 by 8 equals 72 (the Least Common Denominator)..

72 is in fact the least common denominator of 9 and 8 i.d. the first multiple number 9 and 8 have in common.

Why is this done thid way? Let's consider 1/9. This fraction can be seen as rectangle divided in 9 equal regions, 9 equal "stripes", where only 1 of them is shaded.
Now, lets draw a line which cuts those 9 rectangle in the middle. We get immediately 18 regions. Let's continue dividing them in half (equally shaped). And one more time. At the end we will have 72 equal regions. Right? I repeat again. We divided our rectangle consisting in 9 equal "stripes" by 2 (18 regions) then again by 2 (36 regions) and again by 2 (72 regions).
And if you kept staring at pour original shaded zone, you would see it being filled with 2, then 4, then 8 sub-divisions.

Below is the same number line as above but with a "different" naming of the original fractions [4]

Do you see now? By the way, the number "above" (the numerator) is now in the "correct" order: 8 is less than 9. Plus we can "see" that between 8 and 9 there can't be other integers, so there can't be any other fraction with 72 as denominator between 8/72 and 9/72.

This lead us to think that we must keep dividing our imaginary rectangles into more and more regions: 9, 72, 144, 296 until something happens. Here is what happens:

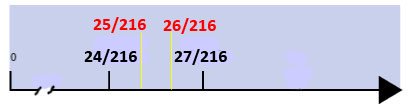
As you can see, eventually we get 3 fractions between 1/9 and 1/8! Namely, 33/296, 34/296, 35/296.

Are there others? Of course there are; an infinity. Litterally.Keep dividing in multiple jumps and you will see.

But coming back to our problem, what about just two fractions between 1/9 and 1/8 as we originally asked?

To find those two fractions, we must look for another kind of fraction with denominator between 144 and 296.

Which one? What about dividing those regions not in half like we did before but in thirds? Of course the denominator must be divisible by three (otherwise we cannot have equal subdivisions of our rectangle; ). And we know from from the divisibility rules that 72 is such a number!

72 x 3 = 216. And so, here we have a new table:

So here we are with solution: 25/216 and 26/216 are the two fractions equally spaced between 1/9 and 1/8

I know, the concept of fractions as measure is not very easy to understand but its' part of the learning curve.

. 1.Ok, theoretically, not all lengths can be numbers, the Greeks knew it already (try to draw a segment which is exactly the square root of 1, that is the diagonal of a square of side equal 1) but for practical purposes, we forget about it for now....(1. The Princeton Companion to Mathematics, page 17, 78))

Source:

2.Elementary and Middle School Mathematics: Teaching Developmentally (7th Edition)

3. Teaching Fractions And Ratios For Understanding: Essential Content Knowledge And Instructional...

4. (in reality, they are still the same fractions; 1/9 and 8/72 are called



equivalent fractions)

From fractions as measure back to basic algebra fractions