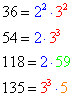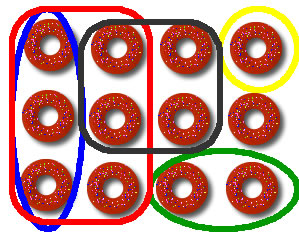
Algebra factoring

Algebra factoring involves an understanding of the two fundamental arithmetics steps of multiplication and division.

Because not even these steps are always self-explanatory, imagine that multiplicaption means "copying" and dividing means "cutting" (an idea by the Italian primary teacher Camillo Bortolato)

So, for instance, the number 12 can be seen in this way: a set of 12 doughnuts

Then, you can think of all possible way of sharing the 12 doughnuts with one or more friends, so dividing them ("cutting" them) in groups of 1, 2, 3, 4 or 6...

Eventually, you realize that the number 12 can be seen as

12= 6 x 2 = 6 + 6
12= 4 x 3 = 4 + 4 + 4
12= 3 x 4 = 3 + 3 +3
12= 2 x 6 = 2 + 2 + 2 + 2 + 2 + 2
12= 1 x 12 = 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 +1 + 1 + 1 + 1

Well, all the numbers which "make up" (by multiplication, i.d. "copying") the number 12 are factors of the number 12.

Factors are also called divisors.

So, 1,2,3,4,6 are factors (or divisors) of the number 12!

A special case of algebra factoring is when we don't find many factors for a number but just two: 1 and the number itself:

For example:

2 = 1 x 2 = 1 + 1

3= 1 x 3 = 1 + 1 + 1

5= 1 x 5 = 1 + 1 + 1 + 1 + 1

7= 1 x 7 = 1 + 1 + 1 + 1 + 1 + 1 + 1

Well, these special numbers are called prime numbers.

All other numbers which do have more factors are called composite numbers instead.

When you want to express a number as a multiplication of prime numbers what you do is actually called a prime factorization of integers.

Eventually, when you carry on factorizing numbers, and you happen to lay before you the results, you notice something evident:

Well, you see that numbers have common factors! That's an important conclusion in algebra factoring.

Dealing with these common factors lead in fact to the very important concept of the Greatest Common Factor and the Least Common Multiple (and so the Least Common Denominator or LCD of a fraction).

From algebra factoring back to homepage